힙이란?
힙은 완전 이진 트리(Complete Binary Tree)의 일종으로,
- 부모 노드 밑에 자식 노드가 최대 2개까지 있을 수 있다.
- 마지막 레벨에 있는 노드를 제외한 모든 레벨 노드가 완전히 채워져 있는 트리 구조이다.
단어 설명 !
부모노드(Parent Node) : 특정 노드의 상위에 위치한 노드
자식노드(Child Node) : 특정 노드의 하위에 위치한 노드
루트노드(Root Node) : 트리구조에서 가장 상위에 위치한 노드
리프노드(Leaf Node) : 트리구조에서 가장 하위에 위치하며 자식 노드가 없는 노드
레벨(Level) : 루트노드부터 시작하여 트리에서 밑으로 몇 번째 층에 있는지를 나타낸다.
(보통 루트노드의 레벨은 0이다)
높이(Height) : 레벨과는 반대로 제일 낮은 리프노드에서부터 시작한다.
루트노드의 높이 = 트리 전체의 높이가 된다.
힙의 종류
- 최대 힙(Max-Heap) : 모든 부모노드가 자식 노드보다 크거나 같은 값을 갖는 특징이 있다.
최대 힙의 이진트리를 보면 루트노드가 가장 큰 값을 가진다. - 최소 힙(Min-Heap) : 모든 부모노드가 자식노드보다 작거나 같다.
최소 힙의 이진트리를 보면 루트노드가 가장 작은 값을 가진다.
밑에 그림은 최대 힙의 트리구조를 보여준다.

이것을 배열 상태로 보게되면

눈치빠르신 분은 아셨겠지만 보통 힙은 배열(Array)를 통해서 구현합니다.
공식은
이진 트리에서 참고해서 보시면
- Left Node(i) = 2 x 1
- Right Node(i) = 2 x 1 + 1
- Parent(i) = floor(i / 2)
공식이 적용됨에 따라 힙을 구현하고 정렬하면 됩니다.
말로하면 직관적으로 와닿지 않으니 코드를 보면서 이해해봐요
(전체적인 구조를 한눈에 파악하기 위해서 클래스를 나누지 않았습니다.)
public class MinHeap {
public static void main(String[] args) {
int[] array = {0, 4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
printHeapArray(build_min_heap(array));
}
//힙 구현
public static int[] build_min_heap(int[] arr) {
int size = arr.length;
int[] heap = new int[size + 1];
System.arraycopy(arr, 0, heap, 1, size);
for(int i = size/2; i >=1 ; i--) {
min_heapify(i,size, heap);
}
return heap;
}
//힙 구조로 재배열 하는 함수
public static void min_heapify(int i,int size, int[] heap) {
int left = 2 * i;
int right = 2 * i + 1;
int smallest;
//왼쪽 자식 노드와 비교
if(left <= size && heap[left] < heap[i]) {
smallest = left;
} else {
smallest = i;
}
//위에서 비교한 값과 오른쪽 자식 노드와 비교
if (right <= size && heap[right] < heap[smallest]) {
smallest = right;
}
//자식 노드가 더 작으면 위치를 바꾸고, min_heapify 재귀호출
if(smallest != i) {
swap(i, smallest, heap);
min_heapify(smallest,size, heap );
}
}
//두 요소의 위치를 바꿈
public static void swap(int i, int j, int[] heap) {
int temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
//힙 배열 출력
public static void printHeapArray(int[] heap) {
for(int i = 1 ; i <= heap.length-1; i++) {
System.out.print(heap[i] + " ");
}
System.out.println();
}
}
그렇다면 힙을 이용한 정렬에 대해 알아보겠습니다.
힙 정렬(Heap Sort)
힙 정렬은 힙을 이용하여 배열을 정렬하는 알고리즘입니다.
- 정렬되지 않은 배열을 최대 힙이나 최소 힙으로 구성한다
- 루트노드를 가장 마지막노드와 교환한다
- 힙 크기를 줄여나간다.
그림으로 먼저 보시면
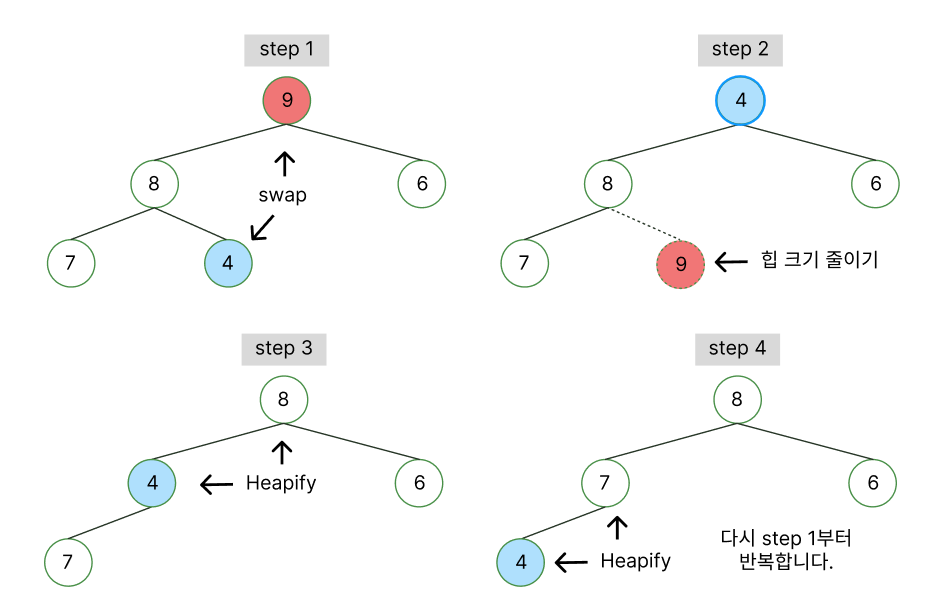
이것을 코드로 구현하면
public static void main(String[] args) {
int[] array = {0, 4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
int size = array.length;
//힙 구현
//printHeapArray(build_min_heap(array));
//힙 정렬
printHeapArray(heapSort(array, build_min_heap(array), size));
}
//힙 정렬
public static int[] heapSort(int[] array, int heap[],int size) {
int j = 0;
for(int i = size; i >= 2 ; i--) {
array[j] = heap[1];
j++;
swap(1,i, heap);
size--;
min_heapify(1,size,heap);
}
array[j] = heap[1];
return array;
}요러한 메서드가 나오게 됩니다.

힙 정렬의 장점
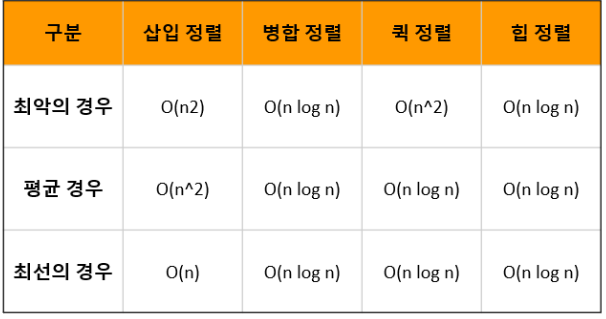
힙 정렬은 퀵 정렬과 마찬가지로 별도의 메모리를 사용하지 않습니다. 이러한 방식을 우리는
제자리 정렬(in-place sorting)이라고 합니다.
따라서 메모리를 사용하지 않으니 일정한 성능을 보여줄 수 있습니다.
*각 원소가 k 위치만큼 떨어져있는 k-sort 배열에서 가장 효율적인 방법으로 사용할 수 있습니다.
힙 정렬의 단점
단점은 숫자가 같은 경우에도 스왑이 일어날 수 있습니다.
때문에 퀵 정렬과 함께 안정적이지 않은 정렬방법 분류가 됩니다.
끝으로..
정렬 알고리즘, 우선순위 큐, 스케줄링 등등 에서도 중요한 역할을 한다고 합니다.
잘알아두자!
'알고리즘' 카테고리의 다른 글
| 분할정복(Divide and Conquer Algorithm)에 대하여 (0) | 2024.07.15 |
|---|---|
| 우선순위 큐(PriorityQueue)에 대하여 (0) | 2024.07.12 |
| 이분 탐색이란(Binary Search)? (0) | 2024.07.08 |
| 그리디 알고리즘에 대하여(Greedy Algorithm) (0) | 2024.07.02 |
| [알고리즘] 이진 탐색 (0) | 2024.02.12 |


